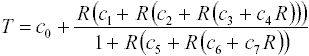RTD Calibration
Relating resistance to temperature
The resistance of an RTD changes almost linearly with temperature. Often, widely available tables are used for converting temperature to resistance and vice versa. (In fact, we include tables you can use for the two most commonly used RTD temperature coefficients. See the Excel file below.)
Conversion of resistance to temperature via an equation offers more flexibility than using a look-up table or chart. The available tabulated values may be curve-fitted to simple equations for the temperature ranges of interest.
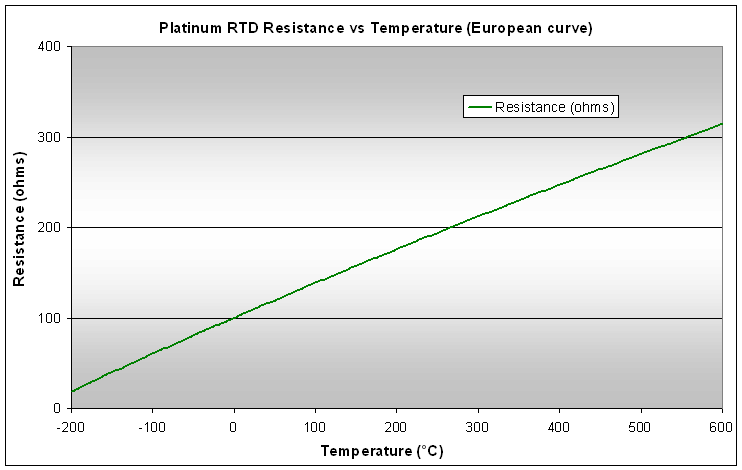
The following graph shows the temperature dependence of RTD resistance for a typical RTD:
RTDs are characterized by their temperature coefficient, α, defined as the average fractional change in resistance per degree Centigrade over a temperature interval of 0°C to 100°C. That is,
α = (R100 – R0)/R0/100°C
See how-do-rtds-work for a discussion of the temperature coefficient of resistance of RTDs.
Depending on the particular alloy of platinum that is used the temperature coefficient may vary from 0.00375 at the low end to 0.003927 for pure platinum, and over time different standards organizations have specified different standard temperature coefficients. The current most common value is α = 0.00385, once known as the "European standard". Some RTDs may still be in use with the value α = 0.003916, known as the "American standard".
When using RTDs, you need to compute temperature from the measured RTD resistance. Depending on the temperature range and accuracy you need, you may use a simple linear fit, quadratic or cubic equations, or a rational polynomial function. We'll discuss each in turn.
Using a linear fit
As an example of a simple equation you might use, for the case of measurements between 0°C and 100°C, you could use a linear approximation as,
T = (R/R0 – 1) / α where R0 = 100, and α = 0.00385
This equation fits a line through the points at 0°C and 100°C (and so has zero error at those temperatures), and has a maximum error in the middle of the range of 0.38°C. The average error over the interval can be minimized by shifting the equation a little, as,
T = (R/R0 – 1)/α - 0.19
to provide a maximum error over the interval of ±0.19°C. In fact, if you are using the RTD over a small temperature range and want good accuracy there you can calibrate by measuring the resistance at the temperature of interest and adding or subtracting a small offset to the computed temperature to force it to equal the calibration temperature.
Using a quadratic fit
A quadratic fit provides a much greater accuracy. A quadratic fit over the range of 0°C to 200°C provides an rms error over the range of only 0.014°C, and a maximum error of only 0.036°C. The equation for a European standard 100Ω RTD is,
T = -244.83 + 2.3419 R + .0010664 R2
You would generally reformulate the above equation to minimize the number of computations as,
T = -244.83 + R ( 2.3419 + .0010664 R )
Using a cubic fit
If you need to measure temperature over a much wider range you can use a cubic fit. A cubic fit over the range of -100°C to +600°C provides an rms error of only 0.038°C over the entire range, and 0.026°C in the range of 0°C to 400°C. The equation is,
T = -247.29 + 2.3992 R + .00063962 R2 + 1.0241E-6 R3
or, using fewer computations,
T = -247.29 + R ( 2.3992 + R (.00063962 + 1.0241E-6 R))
Using a rational polynomial function
If you need to fit the RTD response over a greater range and with greater accuracy than the cubic fit is capable, you can fit RTD data to higher order polynomials. However, rather than using a simple polynomial you should use a rational polynomial function, that is, the ratio of two polynomials.
In general, for the same number of determined parameters and arithmetical operations, rational polynomial functions fit continuous functions more smoothly (that is, with better interpolation) and more accurately than do simple polynomials.1)
Fitting the RTD data over its full range (-200 to +850°C) produces the following formula for computing temperature from RTD resistance,
with the following coefficients,
| co | c1 | c2 | c3 | c4 | c5 | c6 | c7 |
|---|---|---|---|---|---|---|---|
| -245.19 | 2.5293 | -0.066046 | 4.0422E-3 | -2.0697E-6 | -0.025422 | 1.6883E-3 | -1.3601E-6 |
Using the rational polynomial function results in an average absolute error of only 0.015°C over the full temperature range.
Accuracy of the various approximations
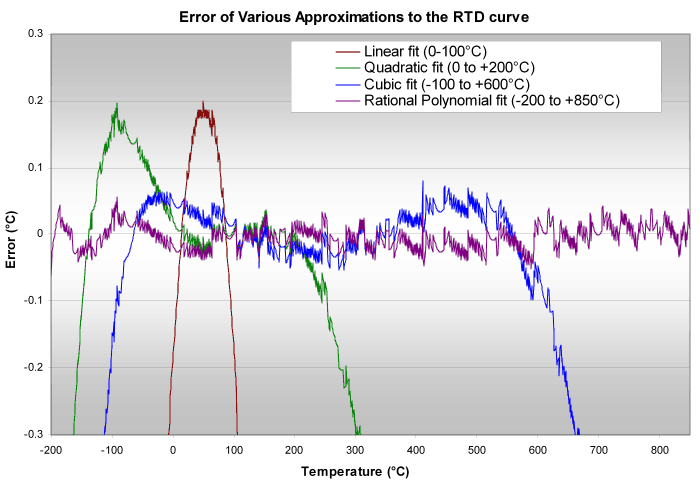
Average absolute errors for the above approximations to the temperature vs resistance RTD curve are summarized in the following table.
| Equation | Temperature range | Average error |
|---|---|---|
| Linear | 0 → +100°C | ± 0.12°C |
| Linear | -200 → +850°C | ± 25°C |
| Quadratic | 0 → +200°C | ± 0.11°C |
| Quadratic | -200 → +850°C | ± 3.2°C |
| Cubic | -100 → +600°C | ±0.03°C |
| Cubic | -200 → +850°C | ± 0.31°C |
| Rational poly | -200 → +850°C | ± 0.015°C |
In each case, for their temperature range of applicability, these errors are less than the tolerance of an off-the-shelf RTD. If you need greater accuracy, you may calibrate the RTD at one or two fixed temperatures, but in that case you will need an independent, accurate temperature measurement at the time of calibration.
The errors of the various calibrations, linear, quadratic, cubic, and rational polynomial function, are shown in the following figure.
The periodic fine jitter in the curve results from rounding errors on the numbers in the resistance vs temperature tables.
Excel spreadsheet for RTD resistance/temperature computations
Here is a link to an Excel spreadsheet containing the computations for the above error graph, as well as resistance vs temperature values for both American and European RTDs.