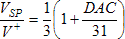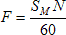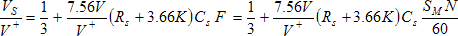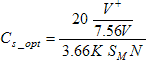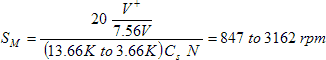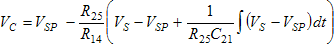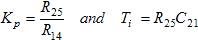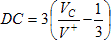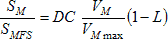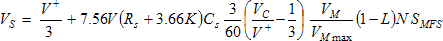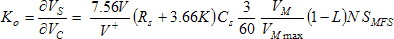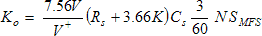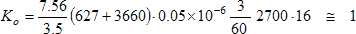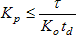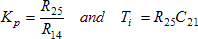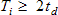Understanding the PI Controller
Optionally control speed with a closed loop proportional-integral controller
With most motors the Motor Control Wildcard should work well out-of-the-box. However, when using some motors or speed encoders you may want to fine tune the gain and response time of the on-board PI controller by changing the values of some components on the board. In that case the discussion on this page will help inform your choices.
Closed-loop vs open-loop control
You can use the Motor Control Wildcard in either of two modes of operation:
- Open-loop motor control – Setting jumper
J3to the Setpoint position (with the jumper cap closer to the potiometer), feeds the 5-bit setpoint signal directly to the motor. You set the motor speed from zero to the maximum by sending a setpoint code from 0 to 31 to the board. That setpoint is translated to a effective average voltage across the motor from zero to the full power supply voltage, VM. The motor speed is roughly proportional to the setpoint you provide, but the actual speed will vary with the power supply voltage if it varies, and with the amount of load placed on the motor. - Closed-loop motor control – Setting jumper
J3to the PI position (with the jumper cap farther from the potiometer), feeds the 5-bit setpoint signal and the measured motor speed to a proportional-integral controller. Its output then controls the average voltage sent to the motor. In closed-loop control variations in motor load or power supply voltage are automatically compensated for; the control loop continuously adjusts power to the motor to maintain a constant measured speed. In this case, the setpoint you provide is translated to motor speed.
For most applications, open-loop control is usually sufficient. DC motors slow down a little as their load is increased, but the slowdown is often modest. If your application isn't subject to power supply voltage fluctuations, and the load is nearly constant (as it often is, for example, for motors driving pumps through gearheads), then open-loop control may be all you need. The advantage of open-loop control is that a potentially unreliable and costly speed sensor isn't needed.
Closed-loop control has the advantage of assuring a constant motor speed despite supply voltage and load variations. It relies on a speed sensor, usually an optical or hall effect sensor, adding a little extra cost to the product.
Basic operation of the closed-loop controller
Fig. 1 diagrams the motor controller, showing the components on the board responsible for the controller's operation.
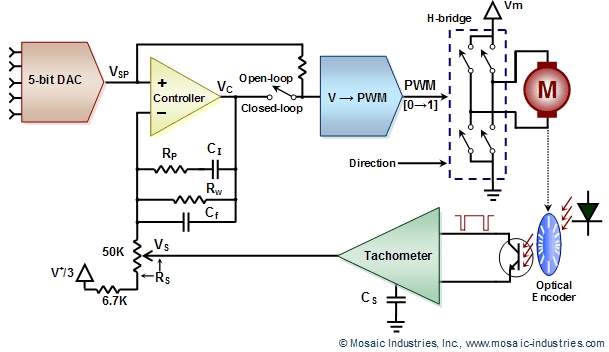
Referring to the figure, a 5-bit digital signal is converted by a DAC to an analog setpoint voltage. In open-loop control (when the onboard jumper, J3, is not installed as illustrated by the Open-loop switch position in the diagram), that setpoint voltage is converted to a 50 KHz PWM signal that is amplified by an H-bridge power driver and applied to the motor. The setpoint is effectively translated to an average motor voltage. As motor speed is directly proportional to the applied voltage, the 32-level setpoint sets the motor speed.
If a jumper cap is placed on jumper position J3, illustrated in the diagram as the Closed-loop position, the control block in the figure is brought into play, providing closed-loop proportional-integral control. A motor speed sensor, or encoder, shown in the figure as an optical interrupter, produces a pulsatile output. Similar magnetic sensors may be used. The sensor produces one or more square wave pules per shaft rotation. A tachometer converts the frequency of pulses into a speed voltage, VS. The components shown in the figure connected to the tachometer govern its gain and response delay.
The PI-controller compares the measured speed, VS, to the setpoint, VSP, producing a control voltage, VC, that is the amplified error between the two. That control voltage is then converted into a PWM signal that ultimately drives the motor. The controller also sums an integral of the error into the control voltage. The gain of the controller and its integration time is set by the passive components shown surrounding the controller: RS, RP, RW, and CI.
The board uses component values that should work well with most motors you may use. The default values are summarized in the following table.
| Component | Default Value | Function |
|---|---|---|
| RS | 50K KΩ pot | Full scale setpoint – Adjust so that when the board is commanded to fully turn ON the motor the motor just barely runs at full speed. For fixed applications RS may be replaced with two fixed resistors, RA and RB. |
| RP | 510 KΩ | RP/RS sets the proportional gain. |
| RW | 10 MΩ | Resets integral gain windup. |
| Cf | 0.1 μF | Filters tachometer ripple for smooth motor speed. |
| CI | 0.1 μF | Provides integral gain. |
| CS | 0.01 μF | Sets the tachometer gain. |
The signals that the controller works with, VSP, VS, and VC, are scaled identically. They all have a minimum of ⅓ of the logic supply voltage (V+ = 3.5 V), corresponding to zero commanded speed, zero actual speed and zero motor drive respectively, and they all have a maximum of ⅔ of the supply voltage, corresponding to full scale commanded speed, full scale actual speed and full scale motor drive.
The following discussion provides details of the properties and interactions of the different blocks shown in Fig. 1 For the purposes of discussion we'll consider an example where we have the following motor properties:
| Motor full scale speed | 2700 rpm (at a full scale supply voltage of VM = 24 V) |
|---|---|
| Encoder pulses | 32 pulses per revolution |
Setpoint signal from the DAC
The DAC accepts a 5-bit number from 0 to 31, and produces a setpoint voltage, VSP, as a portion of the +3.5V supply voltage, V+, as,
The setpoint voltage nominally ranges from ⅓ of the supply to a full scale at ⅔ of the supply. To assure positive shut-off and full-scale, the setpoint voltage actually subceeds and exceeds the ⅓ and ⅔ levels respectively by about ½ of an LSB.
Speed signal from the motor encoder
An onboard tachometer converts the motor speed into a speed signal which can be read as an analog voltage or also used by the board for PI speed control. Just like the setpoint, the speed control voltage ranges from a minimum value of V+/3 (about 1.17V) to a full scale control value of 2V+/3 (about 2.33V). When the motor is not being speed-controlled by the PI loop, greater voltages may be produced with the voltage exceeding 2V+/3, potentially going up to over 7 volts.
The motor’s optical encoder converts the motor’s rotational speed, SM (in rpm), into a frequency, F (in Hz), as,
where N is the number of slots per revolution in the encoder (or for magnetic or other encoders, the number of pulses per revolution). So, for example, for a full scale motor speed of 2700 rpm and an encoder wheel with 32 slots (32 pulses per revolution), the full scale frequency is 1440 Hz.
The tachometer chip produces a speed indicating voltage, VS, proportional to that frequency, but with an offset of ⅓ of the +3.5V supply, as,
where,
- Rs is the speed potentiometer resistance (The resistance between the center tap and lower terminal of the potentiometer in Fig. 1, in series with an effective resistance of 3.66K),
- Cs is the tachometer gain capacitor,
- 7.56V is an internally Zener regulated charging voltage within the tachometer chip,
- V+/3 is a Thevenin equivalent offset voltage produced by a resistor divider in the circuit,
- 6.67K is the Thevenin equivalent impedance of the resistor divider, and,
- F is the motor speed encoder output frequency.
Choosing an optimal tachometer gain capacitor
The gain of the tachometer is proportional to the product of the values of potentiometer resistance (Rs + 3.66 KΩ) and the gain capacitor Cs. A capacitor value is chosen to roughly set the gain, and the potentiometer is then adjusted to more precisely set it. The potentiometer allows a gain variation over a range of 8.5:1 (corresponding to a resistance range of 50+6.67 KΩ to 6.67 KΩ) to accommodate a wide range in top motor speed and/or encoder pulses per revolution.
This speed signal varies from ⅓ of the 3.5V supply voltage, indicating zero speed, to ⅔, indicating full scale. The capacitance should be chosen so that after being rounded down to a realistic value and combined with the smallest resistance (when Rs =0), the full scale VS is caused by a speed a bit greater than the full scale motor speed, for example, 2500 rpm. The potentiometer can then be adjusted to a greater value. Therefore, the optimal CS before rounding down is given by,
For a full scale motor speed of 2700 rpm and a 32-tooth encoder this value is 0.016 µF. A practical value which is the default value used on the board is 0.01 µF. Using this value, the range full scale motor speed, in rpm, corresponding to the full range of the potentiometer, is,
If the potentiometer is adjusted to its minimum value, the full scale VS is produced by a motor speed of 4340 rpm, while increasing the potentiometer resistance to its maximum value increases the tachometer's sensitivity, so that a full scale VS is produced by only 511 rpm. For any setting of the potentiometer, the control signal to the Wildcard allows you to finely control the motor speed from zero up to the maximum set by the potentiometer.
The default value of CS used on the board is 0.01 μF, allowing you to turn Rs to set maximum motor speeds from 511 to 4340 rpm (assuming a 32 slot optical encoder). Different numbers of slots on your optical encoder scale that range proportionally. For example, the following table provides the range of maximum motor speed obtained by setting the potentiometer for different values of encoder slots, N, and tachometer capacitor Cs,
| Cs | N | Maximum speed |
|---|---|---|
| 0.01 μF | 32 | 511 – 4340 rpm |
| 0.01 μF | 16 | 1022 – 8680 rpm |
| 0.1 μF | 8 | 204 – 1736 rpm |
Adjusting the tachometer gain potentiometer
You don't need to do any particular measurement to adjust Rs, just slowly turn the potentiometer while commanding the board for maximum motor speed until the motor speed is the maximum desired.
By way of explanation, with a motor connected and driven at its full speed (or the maximum speed at which you wish to operate it), the potentiometer, Rs, should be adjusted so that the tachometer output is just ⅔ of the +3.5V supply. Ideally, you should choose a motor, motor supply voltage, gearbox and load so that when you are driving the motor open-loop (placing the open-loop/closed-loop jumper J3 in the setpoint position so that the setpoint directly controls the speed) a full scale PWM signal corresponds to the full scale motor speed you want. Then once you adjust the potentiometer, a full scale setpoint produces a full scale motor speed, which produces a full scale speed voltage that matches the full scale setpoint voltage.
For the exemplar motor speed (2700 rpm) and component values used above, pRs would be adjusted to about 4 KΩ. (The potentiometer would be turned so the tap is adjusted to p=4/50=8%.
If the range of Rs is not great enough, then a different value of Cs is required. If the tachometer output is too low, then a greater value of Cs is needed, and if the output is too high over most of the range of Rs, so that only a small portion of the total turning range of the pot is effective, then a smaller Cs is needed.
Choosing the tachometer smoothing capacitance
The tachometer circuit also includes a smoothing capacitor, Cf in the above diagram, to reduce the ripple in its output voltage. The ripple, as a portion of the full range of VS, is approximately 1.6 Cs / Cf. To keep this ripple small, the smoothing capacitor value should greater than or equal to 10× the Cs value. The default value used on the board is 0.1 µF.
The PI controller
The setpoint and speed signals are compared by an op-amp acting as a PI controller. Its output, the control voltage VC, is given by,
Where the resistors and capacitors are the input and feedback circuit elements shown in Fig. 1. The proportional gain, Kp, and integration time, Ti, of the control loop are given by,
The control voltage is then converted to a PWM duty cycle, DC, ranging from 0 to 1, as,
The linear range of VC is from 1/3 to 2/3 of the +3.5V supply. At voltages below V+/3 a zero duty cycle is produced, above 2V+/3 a 100% duty cycle is produced, and in between a proportionate duty cycle is produced.
This duty cycle modulates the power supply voltage applied to the motor, approximately resulting in a full scale motor speed at unity duty cycle. Most practical motors of the size the board is intended to control react to the duty cycle with a time constant of the order of 100-150 msec.
Neglecting for the moment the motor's dynamics, without PI control (that is, running open-loop) the steady-state motor speed, SM (in rpm), is expected to vary with the PWM duty cycle, roughly as,
That is, the speed as a portion of the full scale speed, SMFS, is proportional to the duty cycle, DC, and also to the motor’s supply voltage, VM, as a portion of its maximum value, VMmax, and decreases linearly with the load power extracted from the motor, L.
Closed loop stability
For closed loop control we should choose a gain and integration time for the proportional-integral controller that is matched to the dynamics of the system being controlled, the motor. To do that we need to know three characteristics of the motor: its gain, its delay time, and its ramp-up time.
Motor gain
In control theory the thing being controlled is often called the plant, and its response to the control signal is called the plant gain. For example, if a heater is controlled by a voltage control signal, and a 0-1 volt control signal causes a 0-1000 watt heater output, the plant gain would be 1000 watts per volt. In our schema the plant is everything between the control signal, VC, and the tachometer speed, VS, and the plant gain has units of speed per volt. The plant includes the response of the H-bridge driver, the motor, gearbox and load, and the tachometer's measurement response. To find the gain, we’ll examine the measured steady-state speed as a function of the control voltage, as (combining Equations 2, 9, and Equations 10),
The plant gain, Ko, from the controller’s output voltage VC to the speed indicating voltage, VS, is given by,
If the motor is operated at its specified voltage (VM=VMmax) and unloaded (L=0), we can make the approximation,
Using the exemplar values calculated above when the potentiometer is adjusted so that the full scale value of speed corresponds to the full scale value of motor rpm, this becomes,
That is, the plant gain is simply unity. That shouldn’t be surprising; after all, we chose the tachometer’s gain components (resistor and capacitor) so that the maximum motor speed would correspond to the full scale speed voltage and the full scale control voltage.
While the motor gain is about unity, it is proportional to the motor's power supply voltage and it decreases with the load placed on the motor. It is for these sources of variation that closed-loop control compensates.
Motor response delay
When the motor’s control voltage changes the motor doesn’t respond instantaneously but starts ramping to the new speed after a little delay, usually of a few milliseconds. Further, the speed measurement circuitry necessarily has a small delay. Its response lag, as computed above, is 3.7 to 13.7 msec. That, combined with the motor’s small delay gives us a worst case estimate of a total delay, td, of 15 msec. (In control systems that are characterized by multiple cascaded first order exponential responses, the delay time would be taken as the 2nd most dominant exponential decay time.)
Motor ramp time
The motor has inertia that prevents its instantly assuming a new speed. Instead, the speed ramps up and down with first order exponential decay dynamics to new asymptotic values. Ramp up and down times are different; its ramp up speed depends primarily on its inertia and power supplied and its ramp down time depends on its load and friction. These two times differ the most when the motor is unloaded, in which case the ramp down time can be very long. It’s the shorter, ramp up, time that limits control loop stability. Observations of small motors show times of the order of 100-200 msec. (In control systems that are characterized by multiple cascaded first order exponential responses, the ramp time should be taken as the most dominant, i.e., slowest, exponential decay time.)
Choosing the proportional gain
For any control system the proportional gain must be chosen to prevent instability. As proportional gain is increased, the error between the setpoint and the actual speed decreases. But the gain shouldn’t be increased too much — beyond a threshold value the system starts oscillating. That limit is given by the following equation:
where τ is the motor's response (ramp-up) time, td is its delay time, and Ko is the overall plant gain.
A realistically stable value is about ½ of the limiting value. For our motor parameters, the limit on Kp is about 10, so 5 is a good value to start with if we want to optimize it for a new motor. Because Kp = RP/RS, you can change the proportional gain if necessary by changing RP, recalling that,
Choosing the integration time
The integration term of the P-I control loop allows us to remove almost all steady state error. The integration time should be chosen to be greater than twice the delay time, as,
An integration time much less than this won’t be effective, while an integration time too much greater will cause a slow approach to the steady state speed after a change in setpoint. An upper limit on the integration time, beyond which there is an unnecessarily slow response, is the motor response time, τ.
The integration time is chosen by choosing an appropriate value for the capacitor CI, where Ti = RPCI. First calculate an optimal value, then round it up to the nearest common value.
For many controlled systems, you can increase the proportional gain with the integration term removed until the system just starts oscillating. The delay time can be taken as one half of the observed period.
To limit the wind-up of the integration capacitor in the PI controller there is a parallel resistor, RW, that you can set to be about ten times the feedback resistor, RP.
For further reading →
Image sources →