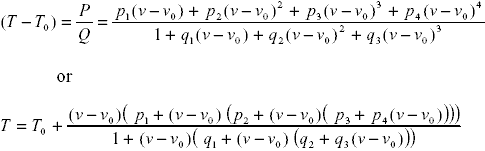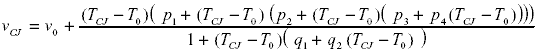Type J Thermocouple Calibration
If you use Mosaic's Thermocouple Wildcard, Type J thermocouple voltage measurements are converted to temperatures for you by the Wildcard's software drivers, and at high accuracy.
But for those of you not using it, but looking for accurate equations for thermocouple voltage to temperature conversion, we hope these thermocouple calibration coefficients are helpful.
Equations for voltage/temperature conversion usually are based on high-order polynomials. The National Institute of Standards and Technology (NIST database of thermocouple values) shows a high order polynomial formula with coefficients curve fitted to Type J thermocouple data they also provide.
However, high order polynomials are often not very accurate – they produce systematic errors as the polynomial oscillates around the fitted data, as shown in these curve fits to Type K thermocouple data.
But there is a better way – using the ratio of two lower order polynomial functions. This page shows you how to convert Type J thermocouple voltage to temperature with rational polynomial functions more efficiently and more accurately than you can using higher order polynomials.
The rational polynomial coefficients provided here produce an order of magnitude lower errors than the NIST ITS-90 type J thermocouple coefficients for direct and inverse polynomials.
Type J calibration equation
A rational polynomial function approximation for Type J thermocouples is used for computing temperature from measured thermocouple potential. The calibration equation uses a ratio of two smaller order polynomials rather than one large order polynomial. Using a least squares curve fitting procedure we fit the National Institute of Standards and Technology (NIST) type J thermocouple data with a rational function of the following form,
where T is the thermocouple temperature (in °C), V is the thermocouple voltage (in millivolts), and To, Vo, and the pi and qi are coefficients. The function uses a ratio of two polynomials, P/Q, in this case a fourth order to a third order polynomial. The second form of the equation emphasizes the most efficient order of operations.
The coefficients, To, Vo, pi and qi were found by performing a least squares curve fit to the NIST data for type J thermocouples. The full temperature range is broken into several sub-ranges, and a different set of coefficients used for each. The coefficients, fitted data and charts of residual errors may be found in this Excel spreadsheet of type J thermocouple data.
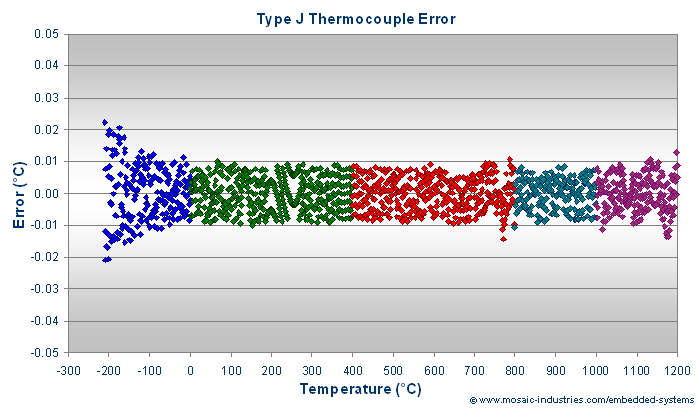
The following table contains calibration coefficients for Type J thermocouple wire. The graph shows residual errors after calibrating the thermocouple with a rational function of polynomials.
| Range | |||||
|---|---|---|---|---|---|
| Voltage: | -8.095 to 0 mV | 0 to 21.840 mV | 21.840 to 45.494 mV | 45.494 to 57.953 mV | 57.953 to 69.553 mV |
| Temperature: | -210 to 0°C | 0 to 400°C | 400 to 800°C | 800 to 1000°C | 1000 to 1200°C |
| Coefficients | |||||
| T0 | -6.4936529E+01 | 2.5066947E+02 | 6.4950262E+02 | 9.2510550E+02 | 1.0511294E+03 |
| V0 | -3.1169773E+00 | 1.3592329E+01 | 3.6040848E+01 | 5.3433832E+01 | 6.0956091E+01 |
| p1 | 2.2133797E+01 | 1.8014787E+01 | 1.6593395E+01 | 1.6243326E+01 | 1.7156001E+01 |
| p2 | 2.0476437E+00 | -6.5218881E-02 | 7.3009590E-01 | 9.2793267E-01 | -2.5931041E+00 |
| p3 | -4.6867532E-01 | -1.2179108E-02 | 2.4157343E-02 | 6.4644193E-03 | -5.8339803E-02 |
| p4 | -3.6673992E-02 | 2.0061707E-04 | 1.2787077E-03 | 2.0464414E-03 | 1.9954137E-02 |
| q1 | 1.1746348E-01 | -3.9494552E-03 | 4.9172861E-02 | 5.2541788E-02 | -1.5305581E-01 |
| q2 | -2.0903413E-02 | -7.3728206E-04 | 1.6813810E-03 | 1.3682959E-04 | -2.9523967E-03 |
| q3 | -2.1823704E-03 | 1.6679731E-05 | 7.6067922E-05 | 1.3454746E-04 | 1.1340164E-03 |
Type J thermocouple accuracy and calibration error
Most of the residual error in the above graph results from rounding of the NIST provided voltage values to the nearest microvolt. You can see the rounding errors as aliasing or Moiré patterns in the data.
The rational function approximation interpolates the data well so that computed values of temperature are more accurate than the residuals plots would indicate.
The Curie point of the iron (770 °C) used in the Type J (iron–constantan) thermocouple causes the excess error apparent in the above graph at 770 °C. Even so, the rational function approximates the curve well and the resulting errors are still quite small for most purposes.
Computing type J cold junction voltages
Your type J thermocouple may be terminated at a cold junction temperature other than 0°C. If so, you must measure the temperature of the cold junction using another sensor, perhaps a thermistor. You can then compute a cold junction voltage from that measured temperature, and use it to compensate the type J thermocouple voltage before converting the thermocouple voltage to a temperature.
In that case you need the inverse transform, that is, an equation for converting temperature into voltage. You don't need a valid equation for a wide temperature range as the cold junction is likely to be placed at ambient temperature. Usually a range of -20 to +70°C is sufficient.
To convert temperature to voltage, you can again use a rational function approximation of the form,
where TCJ is the cold junction temperature, VCJ is the computed cold junction voltage, and the T0, V0, pi and qi are coefficients.
To learn more about cold junction compensation you can consult How To Do Cold Junction Compensation, and you can find the coefficients here: